Abstract
The paper investigates models expressed by equations with higher-grade spatial derivatives which are devised for describing transport phenomena in nanosystems. Particular attention is addressed to the Guyer-Krumhansl equation as a prototype of equations with higher-grade terms. First the thermodynamic consistency of the equation is investigated and conclusions are found for appropriate properties of the coefficients. Next a rather new approach is developed in that evolution equations are not given from the outset but are determined by applying a representation formula that makes the consequences of the second law directly operative. In this approach the free energy, the entropy flux, and the entropy production are considered as constitutive functions that eventually generate the desired evolution equation. Some equations derived in this way prove to be highly non-linear. The approach though leads also to simple models such as the one expressedby the well-known Maxwell-Cattaneo equation.
Keywords
Heat conduction in nanosystems, Higher-grade derivatives, Non-local equations, Guyer-Krumhansl equation
Introduction
In nanoscale systems the heat carrier mean free path may result comparable with the geometric dimensions. While equilibrium properties are well established within statistical mechanics [1], the order of dimensions explains why the literature shows a deep attention to heat transport equations of non-local character at the macroscopic level (see, e.g. [2-4]). Among the approaches involved in the derivation of macroscopic equations it is worth mentioning the recourse to the Boltzmann equation [5], phonon hydrodynamics models [6] or arguments within non-equilibrium thermodynamics [7]. The thermal properties of crystals at low temperatures is often modelled by the Guyer-Krumhansl equations for heat conduction [8]. For definiteness, in the uncoupled harmonic limit the equation for the heat flux reads
![]()
where the superposed dot is the time derivative and ∇ is the gradient operator. Within continuum physics, eq. (1) can be viewed as a rate equation for q where q˙ depends linearly on q itself, a source field r and the second-grade gradients ∇∇q. Owing to the derivation within the kinetic theory and the associated approximations, it is natural to inquire about the thermodynamic consistency within continuum physics. Further, we may look for generalizations suggested by the continuum context. For instance, we may view λ, ν, ζ as constants but even more generally as temperature dependent parameters. Thermodynamically the analysis of (1) is of interest within the so called rational thermodynamics [9] also because so far investigations have been mainly performed through other approaches (see, e.g., [10]). Further, we observe that, in general, the thermodynamic restrictions involve inner products and leave the transverse (orthogonal) parts of vectors or tensors fully undetermined. The application of an appropriate representation formula allows us to look for the general structure of thermodynamically-consistent constitutive equations.This paper has a twofold purpose. First, to examine the validity of the thermodynamic consistency of rate equations like (1) with temperature dependent coefficients. Secondly, to apply the representation formula for the rate q˙ so that a generalization is given of eq.(1) and higher-grade terms, compatible with thermodynamics, are determined.
Representation Formula
The body under consideration occupies the region Ω in the three- dimensional space. Given an origin O, with any point of the body is associated a vector position x. We denote by ∇ = ∂x the gradient operator. For any vector, say f , we define the norm |f | by |f | = (f · f )1/2. The symbol Skw denotes the set of skew-symmetric tensors.
Let w, f be two vectors. Letting ![]() we have
we have
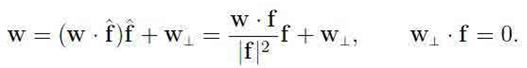
If w is subject to
w · f = g (2)
then
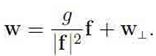
If the transverse part w⊥ is undetermined then we can represent it in the form
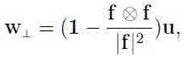
where u is an arbitrary vector. Hence, in view of (2) we can represent w in the form

A number of applications of this representation formula, and of the analogous one for tensors, are developed in refs [11,12].
Thermodynamic Consistency of the Rate Equation
Let ε be the internal energy density, per unit mass, and ρ the mass density. The assumption that the body is rigid makes ρa constant. The balance of energy can be written in the form
![]()
where q is the heat flux, r is the energy supply, and the superposed dot denotes the time derivative.
Let θ be the absolute temperature and η the entropy density. The balance of entropy is expressed by
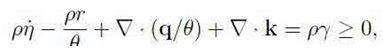
where k is the extra-entropy flux and is the entropy production. Substitution of ρr – ∇.q from the balance of energy (4) and using the free energy
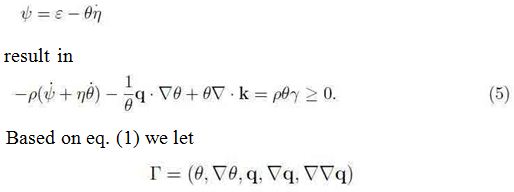
be the set of variables. We then assume η , k, ϒ , q˙ are continuous functions of r and continuously differentiable. Indeed we first let q˙ be given by (1) and allow λ, ν, ζ depend on the temperature θ. Compute ψ and substitute in (5) to obtain
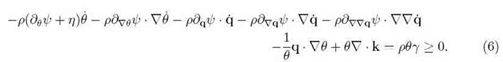
To avoid lengthy calculations we observe that replacing q˙ through (1) leads to
![]()
as far as the dependence on ∇∇θ and ∇∇∇θ is concerned. The arbitrariness and symmetry of ∇∇θ and ∇∇∇θ imply ![]() , in that
, in that
![]()
and the like for ![]() . Though not necessary we put
. Though not necessary we put
![]()
Thus it follows ![]() . Moreover the arbitrariness of
. Moreover the arbitrariness of ![]() and
and ![]() implies
implies
![]()
Hence eq. (6) simplifies to
![]()
which is a restriction on the functions ![]() and λ, ν, ζ For definiteness we let
and λ, ν, ζ For definiteness we let

and ![]() is constant. Hence
is constant. Hence ![]() which is consistent with the condition
which is consistent with the condition ![]() Incidentally, in stationary and uniform conditions
Incidentally, in stationary and uniform conditions ![]() , eq. (1) reduces to the Fourier form
, eq. (1) reduces to the Fourier form
![]()
In light of the results (9) we infer
![]()
thus showing that the heat conductivity ![]() is required to be positive. In addition, the entropy production is
is required to be positive. In addition, the entropy production is
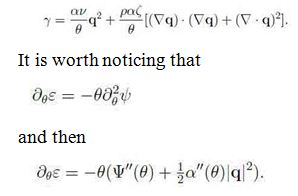
Since ![]() is the specific heat, we guarantee the condition
is the specific heat, we guarantee the condition ![]() by letting
by letting ![]()
In summary, we have considered the rate equation for q, as given from the outset in the form (1), and have determined conditions for the thermodynamic admissibility. Instead, we now start with the Clausius-Duhem inequality (5) and look for possibly more general thermodynamically-consistent rate equations for q.
Generalized Rate Equations
Rate equations are now derived by appealing to the Clausius-Duhem inequality (5) and the representation formula (3). We continue to let ![]() be the set of variables and assume
be the set of variables and assume ![]() Hence eq. (6) reads
Hence eq. (6) reads
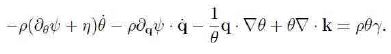
Since ψ, k, and ϒ are independent of ![]() then the arbitrariness of implies again the classical relation
then the arbitrariness of implies again the classical relation
![]()
For definiteness we keep assuming
![]()
Hence it follows that
![]()
We then apply the representation formula (3) with the identifications
![]()
Hence the general representation of q˙ is
![]()
where u is an arbitrary vector-valued function of ![]()
Models with k = 0
If k = 0 then (11) simplifies to
![]()
If also u = 0 then we can write
![]()
In one-dimensional settings (x-direction) we have
![]()
More interestingly, let ![]() Equation (12) becomes
Equation (12) becomes
![]()
The particular case ![]() results in
results in
![]()
that is the Maxwell-Cattaneo equation [13,14] with relaxation time ![]() and heat conductivity
and heat conductivity ![]()
Models with K ≠ O
First we let u = 0 and observe that, by (11), ![]() in a non-linear form.
in a non-linear form.
By analogy with eq. (1) we assume
![]()
where ![]() is the second-order tensor with components
is the second-order tensor with components ![]() . Hence eq. (11) can be written in the form
. Hence eq. (11) can be written in the form
![]()
Notice that
![]()
where the prime 0 means differentiation with respect to temperature.
Hence we obtain
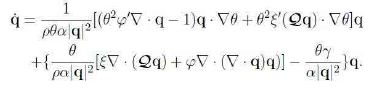
If, rather, we let ![]() be constants then
be constants then ![]() results in the addition of a term proportional to
results in the addition of a term proportional to ![]() but also a term
but also a term ![]() in the expression of q˙ . This shows the qualitative role of u in the formulation of constitutive equations. As an aside, observe that the flux
in the expression of q˙ . This shows the qualitative role of u in the formulation of constitutive equations. As an aside, observe that the flux ![]() is given in [15]; here the whole value of k is established by (9) subject to the constancy of
is given in [15]; here the whole value of k is established by (9) subject to the constancy of ![]()
Conclusions
Models of nanosystems within continuum physics are often established by using highergrade spatial derivatives so as to account for the mean free path of particles comparable with the geometric dimensions. This paper addresses attention to the Guyer-Krumhansl equation (1) as a prototype of equations with higher-grade terms. Owing to the kinetic derivation of (1) it is natural to contrast the equation with the basic requirements of continuum physics. Here this is performed in relation to the thermodynamic consistency namely the compatibility with the second law via the Clausius-Duhem inequality. Definite conclusions are shown to follow if attention is confined to appropriate coefficients ![]() constant along with the requirements (9)).
constant along with the requirements (9)).
Next a rather new approach is developed in that evolution equations are determined by applying a representation formula that makes the consequences of the second law directly operative. In this approach we consider the free energy, the entropy flux, and the entropy production as constitutive functions that eventually generate the desired evolution equation. Some equations derived in this way prove to be highly non-linear.
It seems then that this way is profitable in establishing involved higher-grade equations within continuum physics. The approach though leads also to simple models such as the one expressed by the well-known Maxwell-Cattaneo equation.
Acknowledgments
The research leading to this work has been developed under the auspices of INDAM-GNFM.
References
- Kittel C (1956) Introduction to Solid State Physics, Wiley.
- Zhu CY, You W, Li ZY (2017) Nonlocal effects and slip heat flow in nanolayers. Sci Reports 7:9568.
- Dong Y, Cao BY, Guo ZY (2011) Generalized heat conduction laws based on thermomass theory and phonon J App Phys 110: 063504 (2011).
- Hennessy MG, Myers TG (2020) Guyer-Krumhansl heat conduction in thermoreflectance experiments, in Multidisciplinary Mathematical Modelling. Applications of Mathematics to the Real World, Font and T.G. Myers eds. Springer.
- Xu M, Li X (2012) The modeling of nanoscale heat conduction by Boltzmann transport equation. Int J Heat Mass Transf 55: 1905-1910.
- Alvarez FX, Jou D, Sellitto A (2009) Phonon hydrodynamics and phonon-boundary scattering in J Appl Phys 105: 014317.
- Lebon G (2014) Heat conduction at micro and nanoscales: a review through the prism of Extended Irreversible J Non-Equilib Thermodyn 39: 36-59.
- Guyer RA, Krumhansl JA (1966) Solution of the linearized phonon Boltzmann equation. Phys Rev 148: 766-778.
- Truesdell C (1969) Rational Thermodynamics, A Course of Lectures on Selected Topics, McGraw-Hill, New York.
- Sellitto A, Cimmelli VA, Jou D (2016) Mesoscopic Theories of Heat Transport in Nanosystems. Springer, New York.
- Morro A, Giorgi C (2023) Mathematical Modelling of Continuum Physics, Birchk¨auser, Cham.
- Morro A, Giorgi C (2023) Techniques for the thermodynamic consistency of constitutive equations. Thermo 3: 260-276.
- Straughan B (2011) Heat Waves, Springer, Berlin.
- Joseph DD, Preziosi L (1989) Heat Waves. Rev Mod Phys 61: 41-73.
- Cimmelli VA, Jou D, Ruggeri T, V´an P (2014) Entropy principle and recent results in non-equilibrium theories. Entropy 16: 1756-1807.